Numerical optimization¶
Silent substitution can be approached as a constrained numerical optimization problem of the form:
\begin{equation} \begin{array}{rrclcl} & \underset{x \in \mathbb{R}^{n}}{\text{minimize}} & f(x) \\ & \text{subject to} & g^{L} \le g(x) \le g^{U} \\ & & x^{L} \le x \le x^{U} , \end{array} \end{equation}
where \(x \in \mathbb{R}^{n}\) are the optimization variables (i.e., the primary input weights) whose lower and upper bounds, \(x^{L}\) and \(x^{U}\), are between 0 and 1 to ensure that the solution is within the gamut of the device, \(f(x)\) is the objective function that aims to maximise contrast of the target photoreceptor(s), and \(g(x)\) is a constraint function that calculates contrast for the silenced photoreceptor(s), where \(g^{L}\) and \(g^{U}\) should be zero. In all cases, \(x\) is a vector containing the primary input weights.
pysilsub.problems.SilentSubstitutionProblem has an .optim_solve() method that uses SciPy’s optimisation algorithms to solve a defined problem. By default, it performs a local optimisation with scipy.optimize.minimize using the SLSQP sequential quadratic least squares programming solver.
The objective function, \(f(x)\), and the contrast constraint function, \(g(x)\), are built into the problem class and are conditioned by the values given to the properties.
Basic example¶
[1]:
from pysilsub.problems import SilentSubstitutionProblem as SSP
# Instantiate the problem class
ssp = SSP.from_package_data('STLAB_1_York')
# Define problem
ssp.ignore = ['rh']
ssp.target = ['mel']
ssp.silence = ['sc', 'mc', 'lc']
ssp.target_contrast = .5
ssp.print_problem()
# Find solution
solution = ssp.optim_solve(**{'options':{'disp':False}})
# Plot solution
fig = ssp.plot_solution(solution.x)
# Show device settings
print(f' Background settings: {ssp.w2s(solution.x[0:ssp.nprimaries])}')
print(f' Modulation settings: {ssp.w2s(solution.x[ssp.nprimaries:])}')
************************************************************
*************** Silent Substitution Problem ****************
************************************************************
Device: STLAB_1 (binocular, left eye)
Observer: ColorimetricObserver(age=32, field_size=10)
Ignoring: ['rh']
Silencing: ['sc', 'mc', 'lc']
Targeting: ['mel']
Target contrast: [ 0.5]
Background: None
~~~~~~~~~~~~~~~~~~~~~~~ optim_solve ~~~~~~~~~~~~~~~~~~~~~~~~
> No background specified, will optimise background.
> Performing local optimization with SLSQP.
Background settings: [4085, 1346, 5, 0, 69, 2877, 4094, 3496, 1294, 222]
Modulation settings: [2102, 452, 999, 4036, 4011, 1267, 2098, 3777, 4094, 4069]
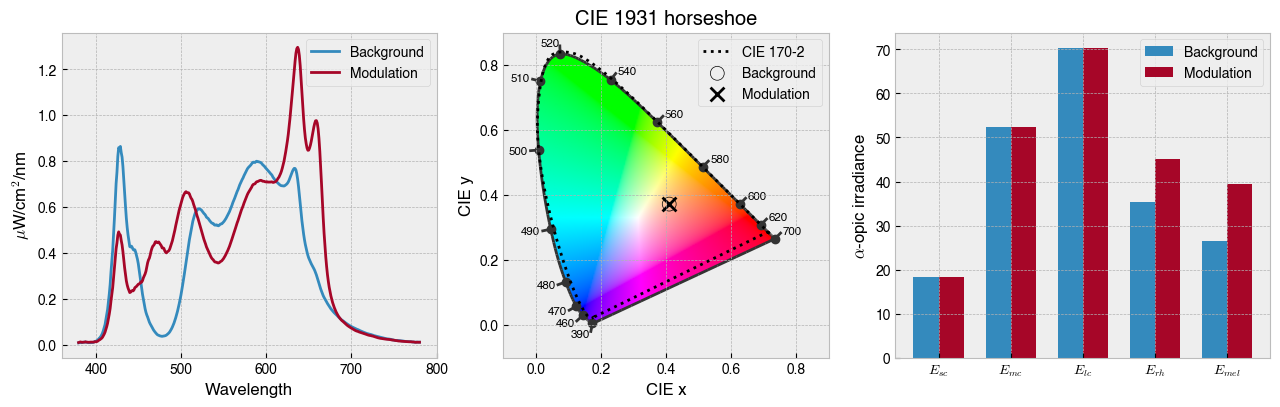
[2]:
# Look at the actual contrast values
ssp.print_photoreceptor_contrasts(solution.x)
sc -0.000051
mc 0.000338
lc -0.000136
rh 0.281317
mel 0.496757
dtype: float64
Maximising contrast¶
If you want .optim_solve(...) to maximise contrast rather than aim for a target value, you can set the target_contrast property to 'max' or 'min'.
[3]:
ssp.target_contrast = 'max'
ssp.print_problem()
# Find solution
solution = ssp.optim_solve(**{'options':{'disp':False}})
# Plot solution
_ = ssp.plot_solution(solution.x)
# Show device settings
print(f' Background settings: {ssp.w2s(solution.x[0:ssp.nprimaries])}')
print(f' Modulation settings: {ssp.w2s(solution.x[ssp.nprimaries:])}')
************************************************************
*************** Silent Substitution Problem ****************
************************************************************
Device: STLAB_1 (binocular, left eye)
Observer: ColorimetricObserver(age=32, field_size=10)
Ignoring: ['rh']
Silencing: ['sc', 'mc', 'lc']
Targeting: ['mel']
Target contrast: [inf]
Background: None
~~~~~~~~~~~~~~~~~~~~~~~ optim_solve ~~~~~~~~~~~~~~~~~~~~~~~~
> No background specified, will optimise background.
> Aiming to maximise contrast.
> Performing local optimization with SLSQP.
Background settings: [2585, 0, 2729, 0, 0, 260, 1951, 3720, 0, 0]
Modulation settings: [0, 0, 3069, 4027, 3058, 0, 0, 3451, 3983, 3969]
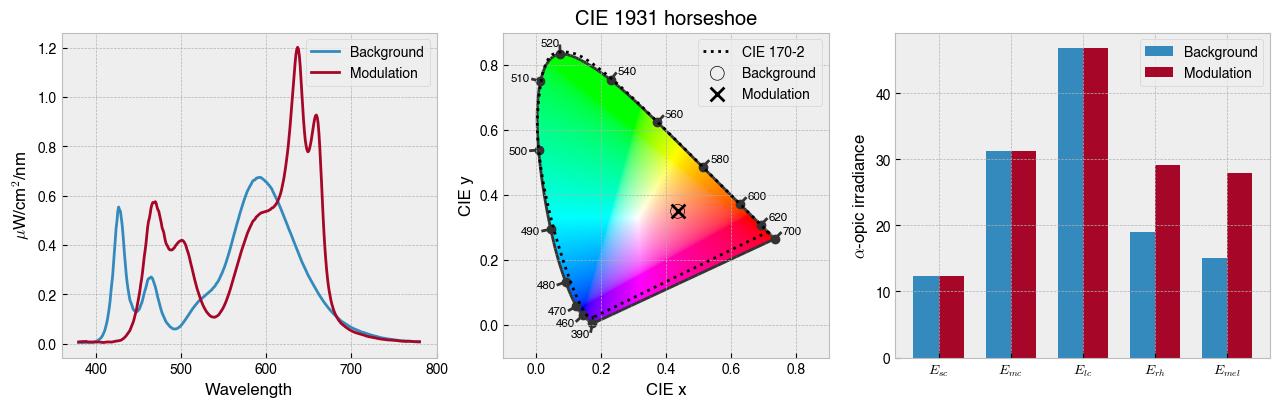
[4]:
ssp.print_photoreceptor_contrasts(solution.x)
sc 0.000023
mc 0.000024
lc -0.000017
rh 0.536400
mel 0.859438
dtype: float64
Specifying a background spectrum¶
Note that in the above examples, both the background and modulation spectra were optimised. However, It often makes sense to stick with a specific background spectrum, particularly if you plan on targeting different photoreceptors in the same experiment. If you specify a background spectrum, .optim_solve() will only optimize the modulation spectrum.
[5]:
ssp.background = [.5] * ssp.nprimaries # All primaries, half-max
ssp.target_contrast = 'max'
ssp.print_problem()
solution = ssp.optim_solve(**{'options':{'disp':False}})
# Plot solution
_ = ssp.plot_solution(solution.x)
# Show device settings
print(f' Background settings: {ssp.w2s(ssp.background)}')
print(f' Modulation settings: {ssp.w2s(solution.x)}')
************************************************************
*************** Silent Substitution Problem ****************
************************************************************
Device: STLAB_1 (binocular, left eye)
Observer: ColorimetricObserver(age=32, field_size=10)
Ignoring: ['rh']
Silencing: ['sc', 'mc', 'lc']
Targeting: ['mel']
Target contrast: [inf]
Background: [0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5]
~~~~~~~~~~~~~~~~~~~~~~~ optim_solve ~~~~~~~~~~~~~~~~~~~~~~~~
> Aiming to maximise contrast.
> Performing local optimization with SLSQP.
Background settings: [2047, 2047, 2047, 2047, 2047, 2047, 2047, 2047, 2047, 2047]
Modulation settings: [2207, 452, 4094, 4030, 3583, 0, 2468, 1403, 4094, 3966]
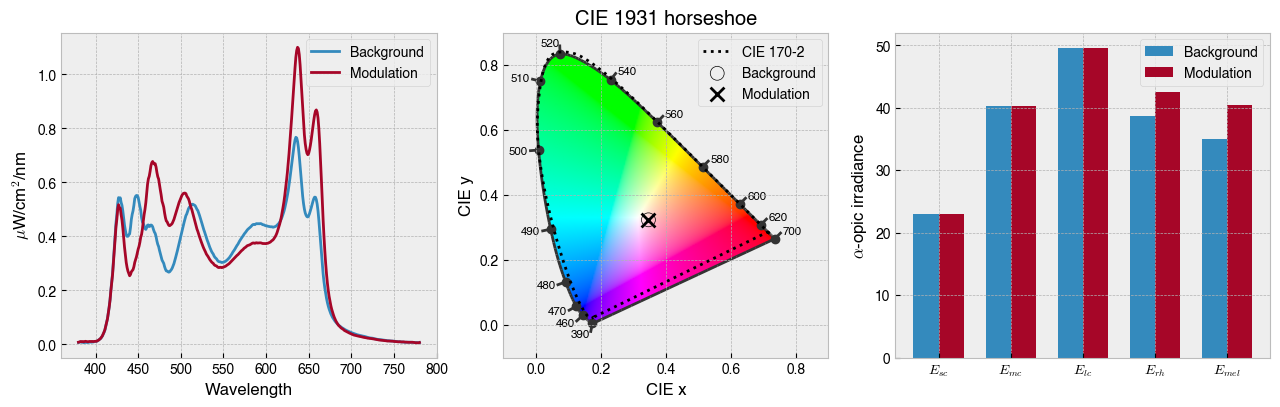
[6]:
ssp.print_photoreceptor_contrasts(solution.x)
sc -0.000002
mc 0.000001
lc -0.000001
rh 0.101365
mel 0.154778
dtype: float64
Note that pinning a background spectrum is a big constraint on the optimisation and is why in this case we only got about 15% contrast on melanopsin.
Local vs. global optimisation¶
By default, .optim_solve() uses Scipy’s minimize function, which is a local minimizer. It starts with an initial random guess (unless told otherwise) for the primary inputs and works from that point to minimize the objective function (which in this case was to maximize contrast).
Due to the random nature of the starting point in the function landscape, the minimum it finds is unlikely to be the global minimum.
If you have enough time, you can tell .optim_solve() to search for the global minimum, in which case it will use Scipy’s basinhopping algorithm to perform a series of local optimisations in conjunction with a global stepping algorithm and return the best solution.
[7]:
ssp.background = None
ssp.print_problem()
solution = ssp.optim_solve(global_search=True, niter=10)
# Plot solution
_ = ssp.plot_solution(solution.x)
# Show device settings
print(f' Background settings: {ssp.w2s(solution.x[0:ssp.nprimaries])}')
print(f' Modulation settings: {ssp.w2s(solution.x[ssp.nprimaries:])}')
************************************************************
*************** Silent Substitution Problem ****************
************************************************************
Device: STLAB_1 (binocular, left eye)
Observer: ColorimetricObserver(age=32, field_size=10)
Ignoring: ['rh']
Silencing: ['sc', 'mc', 'lc']
Targeting: ['mel']
Target contrast: [inf]
Background: None
~~~~~~~~~~~~~~~~~~~~~~~ optim_solve ~~~~~~~~~~~~~~~~~~~~~~~~
> No background specified, will optimise background.
> Aiming to maximise contrast.
> Performing global optimization with basinhopping and SLSQP
basinhopping step 0: f -0.572419
basinhopping step 1: f -1.19937 trial_f -1.19937 accepted 1 lowest_f -1.19937
found new global minimum on step 1 with function value -1.19937
basinhopping step 2: f -1.19937 trial_f -0.739083 accepted 0 lowest_f -1.19937
warning: basinhopping: local minimization failure
basinhopping step 3: f -2.11003 trial_f -2.11003 accepted 1 lowest_f -2.11003
found new global minimum on step 3 with function value -2.11003
warning: basinhopping: local minimization failure
basinhopping step 4: f -2.11003 trial_f -1.26673 accepted 0 lowest_f -2.11003
warning: basinhopping: local minimization failure
basinhopping step 5: f -2.11003 trial_f -0.762291 accepted 0 lowest_f -2.11003
basinhopping step 6: f -1.39862 trial_f -1.39862 accepted 1 lowest_f -2.11003
basinhopping step 7: f -1.69061 trial_f -1.69061 accepted 1 lowest_f -2.11003
warning: basinhopping: local minimization failure
basinhopping step 8: f -1.69061 trial_f -1.02817 accepted 0 lowest_f -2.11003
basinhopping step 9: f -1.72187 trial_f -1.72187 accepted 1 lowest_f -2.11003
basinhopping step 10: f -1.72187 trial_f -0.888427 accepted 0 lowest_f -2.11003
Background settings: [2145, 0, 0, 0, 0, 0, 0, 3212, 0, 0]
Modulation settings: [65, 36, 801, 2730, 468, 0, 0, 1976, 3262, 4010]
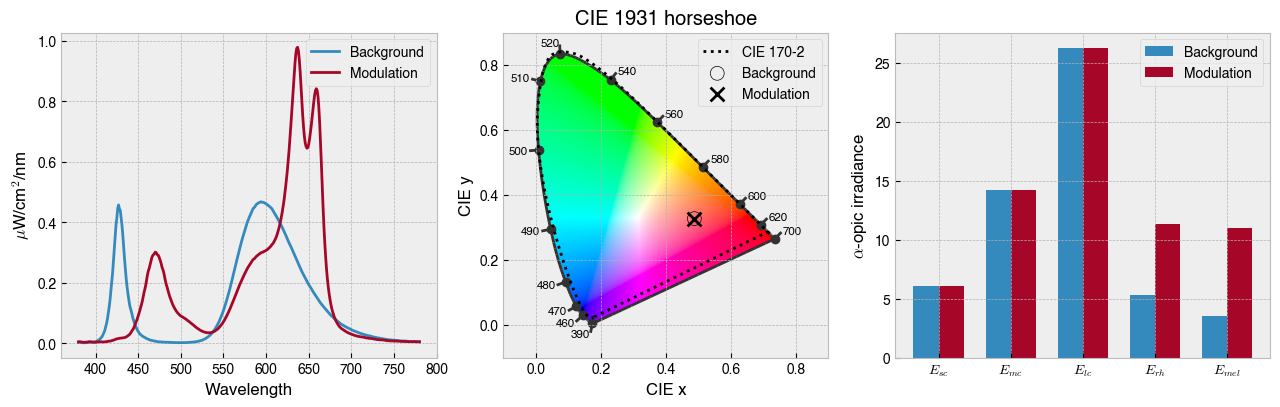
[8]:
ssp.print_photoreceptor_contrasts(solution.x)
sc -0.000035
mc 0.000030
lc -0.000041
rh 1.120994
mel 2.110031
dtype: float64
211% melanopic contrast!
